Si­cher­heit sowie einer Steigerung des Komforts. Für eine vorrausschauende Fahrweise müssen zukünftige Fahrfunktionen das dynamische Umfeld prädizieren und darüber hinaus die eigene Bewegung des Fahrzeugs planen. Innerhalb der Architektur automatisierter Fahrzeuge ergibt sich daraus eine besondere Rolle für den Bereich der Trajektorienplanung. Die Herausforderung ist es unter Berücksichtigung der Fahrdynamik und in Abhängigkeit von der momentanen Verkehrssituation eine kollisionsfreie Trajektorie zu finden, welche die geltenden Verkehrsregeln beachtet.

Verknüpfung von Kurveninterpolations- und Optimierungsverfahren

Die splinebasierte Trajektorienplanung nutzt eine Interpolationsstrategie unter der Annahme, dass innerhalb jedes Splineintervals eine ausreichend genaue Approximation des automatisierten Manövers vorliegt. Durch die Interpolation kann die Anzahl an benötigten Optimierungsvariablen innerhalb des kontinuierlichen Optimierungsverfahrens verringert werden, wobei die Auflösung der Trajektorie von der Interpolation unabhängig gewählt werden kann. Dadurch kann die Effizienz zur Lösung des Trajektorienplanungsproblems gesteigert werden. Das Verfahren kombiniert die Stärken eines Optimierungsverfahrens mit denen der Kurveninterpolation. Dazu wird ein Spline in ${}^{F}x(t)$ und ${}^{F}y(t)$ definiert. In Abhängigkeit der Interpolationsordnung werden über die Anfangs- und Endbedingungen, sowie den Kontinuitätsbedingungen zwischen zwei Zeitintervallen die Splinekoeffizienten bestimmt. Zur Bestimmung des optimalen Übergangszeitpunktes von einem Interval zum nächsten, werden die Zeitpunkte ebenfalls optimiert. Aufgrund der splinebasierten Formulierung kann die Trajektorie als zeitkontinuierlich betrachtet werden, welches die Wahl der zeitlichen Auflösung unabhängig von den Stützstellen und dem Prädiktionshorizont erlaubt. Durch Interpolation werden die Trajektorienpunkte errechnet, welche die Trajektorie des Ego-Fahrzeugs ergeben.

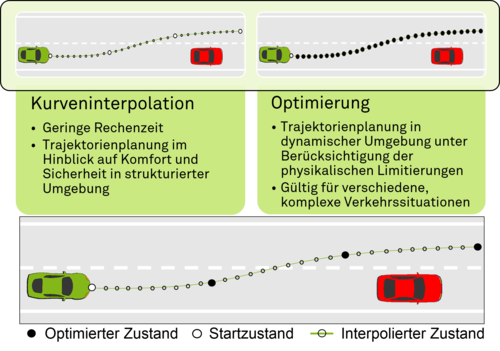
Kombination von diskreter und kontinuierlicher Optimierung

Der Nachteil welcher mit kontinuierlichen Optimierungsverfahren zur Trajektorienplanung einhergeht ist, dass anhand der Problemformulierung das Auffinden eines lokalen Minimums als optimale Lösung nicht ausgeschlossen werden kann. Zur Vermeidung lokaler Minima können als Erweiterung graphenbasierte Verfahren herangezogen werden, welche der Optimierung vorangehen und            eine geeignete Initialisierung vornehmen. Graphenbasierte Verfahren erzeugen in einem ersten Schritt einen Graphen, welcher die Kosten für das jeweilige Manöver beinhaltet.  Zur Erzeugung des Graphen können zum einen die Stellgrößen und zum anderen der Zustandsraum diskretisiert werden. In einem zweiten Schritt wird die Trajektorie über ein Graphensuchverfahren als der Zweig mit den geringsten Kosten bestimmt. Die Herausforderung bei diesem Vorgehen liegt in der Erzeugung eines Graphen, welcher für die vorliegende Situation eine geeignete Trajektorie enthalten muss. In Bezug auf die Optimalität der Trajektorie ist ersichtlich, dass die Lösung dieses Verfahrens lediglich auflösungvollständig ist, da eine Diskretisierung des Zustandsraumes vorgenommen werden muss. Eine feinere Diskretisierung steht dabei einer längeren Rechenzeit gegenüber. Über die Verknüpfung mit einer nachfolgenden kontinuierlichen Optimierung kann eine wesentlich gröbere Diskretisierung des Zustandsraumes vorgenommen werden ohne schon im Vorfeld die optimale Lösung durch die Wahl der Beispieltrajektorien ausgeschlossen zu haben. Das diskrete Verfahren kann im ersten Schritt dazu verwendet werden, um eine geeignete Initialisierung der Trajektorie vorzunehmen. Im weiteren Verlauf wird die Trajektorie optimiert und anschließend an den Trajektorienfolgeregler übergeben. Für den nächsten Schritt kann nun nach dem Prinzip des Warmstarts die optimierte Trajektorie als neue Initialisierung gesetzt werden. Dabei kann angenommen werdem, dass die Trajektorie weiterhin der global optimalen Lösung entspricht. Um auszuschließen, dass dises Annahme nicht erfüllt ist, kann zyklisch die Lösung des diskreten Verfahrens mit der Lösung des kontinuierlichen Verfahrens verglichen werden. Sollte die optimale Trajektorie des diskreten Verfahrens eine bessere Lösung im Sinne des Optimalitätskriteriums darstellen als die durch kontinuieriche Optimierung erhaltene Lösung wird eine Aktualisierung der initialen Trajektorie durch das diskrete Verfahren vorgenommen. Dadurch kann sichergestellt werden, dass auch für den Fall das die kontinuierliche Optimierung in ein lokales Optimum konvergiert weiterhin die Möglichkeit besteht durch eine Neuinitialisierung das globale Optimum zu finden.

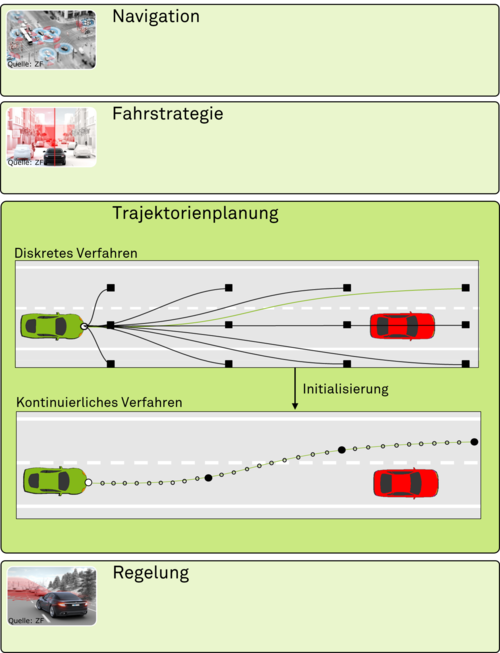
Trajektorienplanung in der Architektur automatisierter Fahrzeuge

Innerhalb der Architektur automatisierter Fahrzeuge kann die Trajektorienplanung als ein Teilmodul angesehen werden, welches anhand der Anforderungen aus der Fahrstrategie eine Trajektorie bestimmt. Dabei muss neben den Vorgaben der statischen Routenplanung in der Navigationsschicht auch die Umgebungssituation des Ego-Fahrzeugs berücksichtigt werden. Anschließend wird die geplante Trajektorie durch ein entsprechendes Modul zur Regelung umgesetzt. Das Fahrzeug muss somit in der Lage sein, durch die Übernahme der Längs- und Querführung, der vorgegebenen Solltrajektorie zu folgen.  Für die Anwendung werden im besonderen Maße Regelungssysteme benötigt, welche die Fahrzeugdynamik ganzheitlich über alle Bereiche der Fahrdynamik hinweg betrachten. Eine Herausforderung stellt dabei die Kopplung zwischen Quer- und Längsdynamik dar, welche vor allem bei hohen Quer- und Längsbeschleunigungen nicht zu vernachlässigen ist.

Das Projekt wird in Kooperation mit der ZF Group durchgeführt.