Modellierung und Regelung elastischer Leichtbauroboter mit mehreren Schwingungsebenen

Forschungsziele
Für eine sichere physische Mensch-Roboter-Interaktion werden zunehmend Leichtbauroboter in Betracht gezogen. Strukturelastizitäten ermöglichen dabei durch geringeres Gewicht und inhärente Sicherheit eine Gefahrenreduktion. Sie gehen allerdings mit Schwingungen und lastabhängigen Verbiegungen einher.
Diese vermeintlichen Nachteile können durch geschickte Regelung jedoch zum Vorteil genutzt werden, beispielsweise zur Kraftdetektion. Bisherige Arbeiten zu elastischen Roboterarmen zielen hauptsächlich auf Modellbildung, Schwingungsdämpfung und Bahnplanung ab, wobei zumeist nur eine Schwingungsebene betrachtet wird. Existieren mehrere Schwingungsebenen, wie es in realen Anwendungen üblich ist, wird die Steuerbarkeit der zugehörigen Schwingungen mittels vorhandener Aktoren fraglich.
Ziel des Forschungsvorhabens ist aufbauend auf vorangegangenen Projekten (siehe Link) die Entwicklung von verschiedenen Steuerbarkeitsmaßen sowie Regelungs- und Konstruktionskonzepten, die zunächst eine erfolgreiche Schwingungsdämpfung ermöglichen, später aber auch über diese hinausgehen und Nutzen aus der inhärenten mehrdimensionalen Nachgiebigkeit strukturelastischer Serialkinematiken ziehen.
Experimentalsystem TUDORA
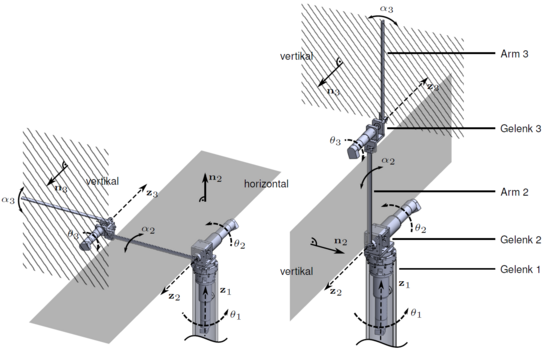
Zur Validierung der Ergebnisse dient der intern entwickelte Leichtbauarm TUDORA (TU Dortmund Omni-elastic Robot Adapted) mit drei Freiheitsgraden. Abbildung 1 zeigt den relevanten mechanischen Aufbau sowie die Schwingungsebenen der zwei elastischen Armkörper und verdeutlicht die konfigurationsabhängige Steuerbarkeit.
Forschungsergebnisse
Steuerbarkeit und Erreichbarkeit
Zur Herleitung der modalen Steuer- und Erreichbarkeit von Schwingungen werden die Gleichungen der elastischen Bewegungen des betrachteten Roboterarms aufgestellt. Diese werden anschließend unter Voraussetzung kleiner elastischer Verformungen auf den statischen Fall und die horizontale Ebene reduziert. Es ergeben sich Steuerbarkeitsmatrix Smod und -maß smod sowie Erreichbarkeitsmatrix und -maß . [Konno u. a. (1997) „Configuration-dependent vibration controllability of flexible-link manipulators“]
Für die Betrachtung jeder Konfiguration gilt: Sind alle strukturellen Schwingungsmoden erreichbar, so ist auch die Steuerbarkeit der Schwingungen gegeben. Ist die Konfiguration hingegen nicht steuerbar hinsichtlich der Schwingungen, so ist mindestens eine strukturelle Schwingungsmode nicht erreichbar.
Diese Vorgehensweise führt zu aufwendigen Berechnungen und dient lediglich der Vermeidung nicht-steuerbarer Roboterkonfigurationen.
Abbildung 2 zeigt die Ergebnisse des modalen Ansatzes für das Experimentalsystem TUDORA. Der Einfluss der Kopplungen zwischen den einzelnen Gelenk-Armkörper-Modulen steigt dabei nichtlinear mit der Nutzlast, während die zu vermeidenden Minima unabhängig von der Nutzlast sind. Zu beachten ist, dass bereits „zu kleine“ Werte eine Schwingungsdämpfung gefährden.
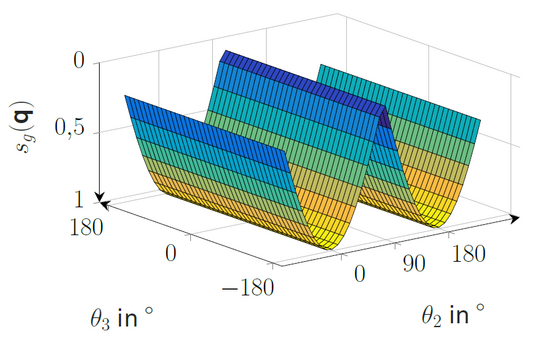
Alternativ wird die geometrische Steuerbarkeit strukturelastischer Schwingungen untersucht. Diese berücksichtigt die Relativorientierungen aller Gelenkachsen zu jeweils allen Schwingungsebenen. Unter der Voraussetzung kleiner elastischer Verformungen genügt zunächst die Betrachtung der äquivalenten Starrkörperkinematik. Es ergeben sich Steuerbarkeitsmatrix Sg und -maß sg, die für die untersuchte Konfiguration unabhängig von der Nutzlast eine eindeutige Zuordnung des Einflusses jedes Aktors auf jeweils jede Schwingung erlauben. Abbildung 3 zeigt die Ergebnisse des geometrischen Ansatzes für das Experimentalsystem TUDORA.
Der Verlauf bezüglich ähnelt dem der modalen Steuer- und Erreichbarkeit (insbesondere hinsichtlich der ersten Schwingungsmode von Arm 2). Die einhergehende Normierung des Steuerbarkeitsmaßes auf [0; 1] lässt dabei die Festlegung eines Schwellwertes unabhängig vom spezifischen Roboterarm zu. Bei Wahl geeigneter Schwellwerte entsprechen sich die ermittelten (nicht-)steuerbaren Konfigurationen beider Ansätze.
Modellfreie Schwingungsdämpfung
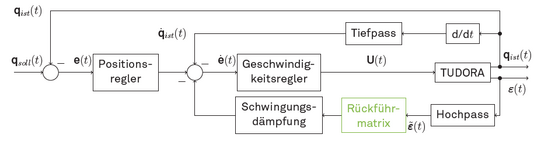
Das geometrische Steuerbarkeitsmaß eignet sich darüber hinaus zur Erweiterung von Regelungskonzepten zur Schwingungsdämpfung auf Systeme mit mehreren Schwingungsebenen. Hierfür werden beispielsweise entsprechend Abbildung 4 die mittelwertfreien Dehnungsmessungen zurückgeführt und dem Aktor mit der jeweils größten Einflussmöglichkeit gemäß ihrer geometrischen Steuerbarkeit zugeordnet.
Alternative Regelungskonzepte der Schwingungsdämpfung und der Endeffektorpositionierung sowie die Ableitung einer konstruktionstechnischen Optimierung sind Gegenstand aktueller Forschung.
Wir bedanken uns für die finanzielle Unterstützung des Projekts durch die Deutsche Forschungsgemeinschaft (DFG, BE 1569/12-1).
Referenzen
- Krämer, M., F. I. Muster, C. Rösmann, and T. Bertram: An optimization-based approach for elasticity-aware trajectory planning of link-elastic manipulators, Mechatronics, vol. 75, 2021.
- Krämer, M., F. I. Muster, C. Rösmann, and T. Bertram: Elasticity-Aware Online Motion Optimization for Link-Elastic Manipulators, IFAC-PapersOnline, vol. 53, no. 2, pp. 9980–9985, 2020
- J. Malzahn. „Modeling and control of multi-elastic-link robots under gravity“. Diss. TU Dortmund, 2014.
- F. I. Muster, M. Krämer und T. Bertram. „Trajektorienplanung für einen strukturelastischen Leichtbauroboter mit mehreren Schwingungsebenen”. In: IFToMM D-A-CH Konferenz. 2020.
- F. I. Muster, J. Malzahn und T. Bertram. „Exploiting Controllability for Vibration Damping in Multiple Planes of Link-Elastic Robot Arms”. In: IEEE International Conference Mechatronics (ICM). 2019.
- F. I. John, J. Malzahn und T. Bertram. „Vergleich von Steuerbarkeitsmetriken anhand eines strukturelastischen Roboterarms mit mehreren Schwingungsebenen“. In: IFToMM D-A-CH Konferenz. 2018.
- F. I. John, J. Malzahn und T. Bertram. „Controllability and accessibility of vibrations in multiple planes on link-elastic robot arms“. In: ROBIO. IEEE. 2017, S. 1491–1496.
- F. I. John, J. Malzahn und T. Bertram. „Strukturelastische Roboterarme mit mehreren Schwingungsebenen“. In: Fachtagung Mechatronik. VDE. 2017, S. 162–167.