Detail_TUDORA

Modeling and control of elastic lightweight robots with multiple vibration planes.

Research Objectives Lightweight robots are increasingly being considered for safe physical human-robot interaction. In this context, structural elasticities enable hazard reduction due to lower weight and inherent safety. However, they are accompanied by vibrations and load-dependent bending. However, these perceived disadvantages can be turned to advantage through clever control, for example for force detection. Previous work on elastic robot arms has mainly focused on modeling, vibration damping and path planning, mostly considering only one vibration plane. If several vibration planes exist, as is common in real applications, the controllability of the associated vibrations by means of existing actuators becomes questionable.

Building on previous projects (see link), the goal of the research project is to develop various controllability measures as well as control and design concepts that initially enable successful vibration damping, but later also go beyond this and take advantage of the inherent multidimensional compliance of structurally elastic serial kinematics.

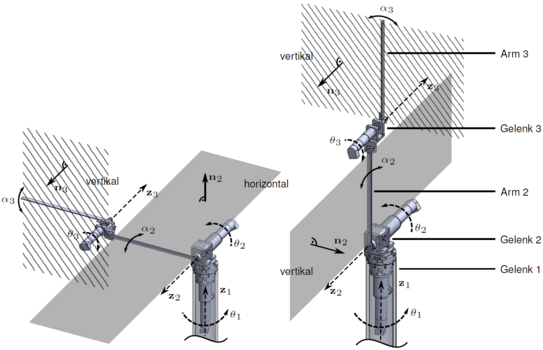
TUDORA experimental system

Abbildung 1: Experimentalsystem TUDORA in zwei Konfigurationen. Links: Sehr gute Steuerbarkeit erwartet, Rechts: Schlechte Steuerbarkeit erwartet.

The internally developed lightweight arm TUDORA (TU Dortmund Omni-elastic Robot Adapted) with three degrees of freedom is used to validate the results. Figure 1 shows the relevant mechanical structure and the vibration planes of the two elastic arm bodies and illustrates the configuration-dependent controllability.

Research results

Controllability and reachability

To derive the modal controllability and reachability of oscillations, the equations of the elastic motions of the robot arm under consideration are set up. These are then reduced to the static case and the horizontal plane under the condition of small elastic deformations. Controllability matrix_smod and -measure_smod as well as reachability matrix and -measure . [Konno et al. (1997) "Configuration-dependent vibration controllability of flexible-link manipulators"].

For the consideration of each configuration, if all structural vibration modes are reachable, then the controllability of the vibrations is also given. If, on the other hand, the configuration is not controllable with respect to the vibrations, then at least one structural vibration mode is not reachable.

This approach leads to costly calculations and only serves to avoid non-controllable robot configurations.

Figure 2 shows the results of the modal approach for the experimental system TUDORA. The influence of the couplings between the individual joint-arm body modules increases nonlinearly with the payload, while the minima to be avoided are independent of the payload. It should be noted that even "too small" values endanger vibration damping.

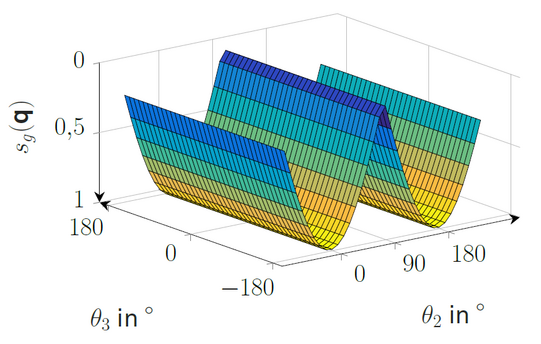
Alternatively, the geometric controllability of structurally elastic vibrations is investigated. This takes into account the relative orientations of all joint axes to all vibration planes in each case. Under the condition of small elastic deformations, the consideration of the equivalent rigid body kinematics is sufficient at first. The result is a controllability matrix Sg and a controllability dimension sg, which allow an unambiguous assignment of the influence of each actuator on each vibration for the investigated configuration independent of the payload. Figure 3 shows the results of the geometric approach for the experimental system TUDORA.

Abbildung 2: Modale Steuerbarkeit von TUDORA mit 0,5 kg Nutzlast.

Abbildung 3: Geometrische Steuerbarkeit von TUDORA.

The course with respect to is similar to that of the modal controllability and reachability (in particular with respect to the first oscillation mode of arm 2). The accompanying normalization of the controllability measure to [0; 1] allows the definition of a threshold value independent of the specific robot arm. If suitable threshold values are chosen, the determined (non-)controllable configurations of both approaches correspond to each other.

Model free vibration damping

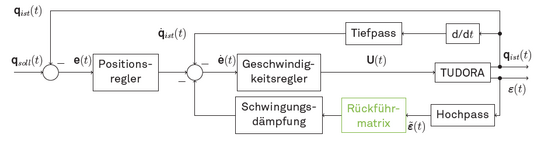
The geometric controllability measure is also suitable for extending control concepts for vibration damping to systems with several vibration levels. For this purpose, for example, the mean value-free strain measurements are fed back according to figure 4 and assigned to the actuator with the greatest influence possibility in each case according to their geometric controllability.

Figure 4: Simplified block diagram of the control loop with feedback matrix. [cf. Malzahn (2014) "Modeling and control of multi-elastic-link robots under gravity"].

Alternative control concepts of vibration damping and end effector positioning as well as the derivation of a design optimization are the subject of current research.

We gratefully acknowledge the financial support of the project by the German Research Foundation (DFG, BE 1569/12-1).

References

J. Malzahn. "Modeling and control of multi-elastic-link robots under gravity". Diss. TU Dortmund University, 2014.

F. I. Muster, M. Krämer, and T. Bertram. "Trajectory planning for a structurally elastic lightweight robot with multiple vibration planes." In: IFToMM D-A-CH Conference. 2020.

F. I. Muster, J. Malzahn, and T. Bertram. "Exploiting Controllability for Vibration Damping in Multiple Planes of Link-Elastic Robot Arms." In: IEEE International Conference Mechatronics (ICM). 2019.

F. I. John, J. Malzahn, and T. Bertram. "Comparison of controllability metrics using a structural elastic robot arm with multiple vibration planes." In: IFToMM D-A-CH Conference. 2018.

F. I. John, J. Malzahn, and T. Bertram. "Controllability and accessibility of vibrations in multiple planes on link-elastic robot arms." In ROBIO. IEEE. 2017, S. 1491-1496.

F. I. John, J. Malzahn, and T. Bertram. "Structurally elastic robotic arms with multiple vibration planes." In: Symposium on Mechatronics. VDE. 2017, pp. 162-167. detail page TUDOR.