Vergleich von Bahnparametrisierungen und die Berücksichtigung von Nebenbedingungen hinsichtlich der entstehenden Optimierungsprobleme

In vielen Fällen wird die Trajektorienoptimierung mit einer diskreten Anzahl an Positionen entlang der Trajektorie als Entscheidungsvariablen durchgeführt. In verschiedenen Publikationen wird diese Parametrisierung für die Ausführung von Autobahnmanövern oder die Planung von Notfalltrajektorien verwendet. Ein Vorteil ist ihre Flexibilität, die es erlaubt, verschiedene Szenarien zu lösen. Jedoch erfordern nicht alle Situationen eine Parametrisierung mit so vielen Freiheitsgraden. Insbesondere bei der Ausführung von Autobahnmanövern reicht eine geringere Anzahl von Entscheidungsvariablen aus. Da aus der verwendeten Optimierung über eine endliche Menge an Positionen Größen höherer Zeitableitung mithilfe von finiten Differenzen ermittelt werden, was im Folgenden als Finite Difference Parameterization (FDP) bezeichnet wird, ist eine Vergrößerung der Zeitabstände zwischen den Positionen möglicherweise nicht immer sinnvoll. Dieser Umstand motiviert die Spline-Parametrisierung von Trajektorien. Es erlaubt die Beschreibung von Trajektorien in einer zeitkontinuierlichen Weise durch einen endlichen Satz von Parametern. Jeder polynomiale Spline kann äquivalent durch eine Linearkombination von Basisfunktionen beschrieben werden, die als B-Spline bezeichnet wird. Dieser ist von einer konvexen Hülle umschlossen. Die Eigenschaft der konvexen Hülle bietet die Möglichkeit, die Erfüllung von Nebenbedingungen über die zeitkontinuierliche Trajektorie zu garantieren. Wird die unendliche Zahl der Nebenbedingungen mithilfe der konvexen Hülle auf eine endliche Anzahl reduziert wird von der B-Spline-Relaxation gesprochen. Im Gegensatz dazu garantiert der häufig verwendete Multiple Interference Test die Erfüllung von Nebenbedingungen nur an bestimmten Zeitpunkten entlang der Trajektorie.

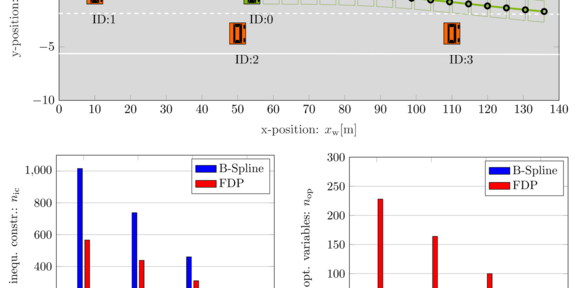
Um einen Eindruck von den Problemformulierungen zu erhalten, die sich aus der FDP- und der B-Spline-Parametrisierung ergeben, wird die Anzahl der Ungleichheitsnebenbedingungen und Optimierungsvariablen in Abhängigkeit von der Anzahl der Hindernisfahrzeuge in einem Autobahnszenario verglichen. Um Kollisionen mit Hindernisfahrzeugen zu vermeiden, wird das Separating Hyperplane Theorem verwendet, das zusätzliche Ungleichungheitsnebenbedingungen und Optimierungsvariablen pro Hindernisfahrzeug einführt. Die B-Spline-Parametrisierung führt in Verbindung mit der B-Spline-Relaxation zu einer reduzierten Anzahl von Optimierungsvariablen im Vergleich zur FDP-Parametrisierung unter Verwendung des Multiple Interference Tests. Auf der anderen Seite wird die Anzahl der Ungleichheitsnebenbedingungen für eine zunehmende Anzahl von Hindernissen höher.