Robustness Analysis of a 2-Degrees of Freedom Linear Quadratic Gaussian Position Control (2DOF LQG Control) of the Front Axle Actuator for a Steer-by-Wire Steering System

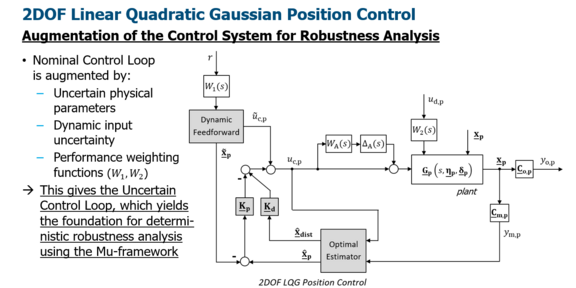
The Steer-by-Wire (SbW) steering system is a key technology for highly automated driving. For automated lateral vehicle guidance, the precise position control of the SbW Front Axle Actuator represents an essential prerequisite. For fulfilling the high requirements to reference tracking, disturbance rejection, stability, and robustness a Two-Degrees-of-Freedom Linear Quadratic Gaussian Position Control (2DOF LQG Control) was developed. This control allows an independent design of the command response and the disturbance response of the closed loop system.

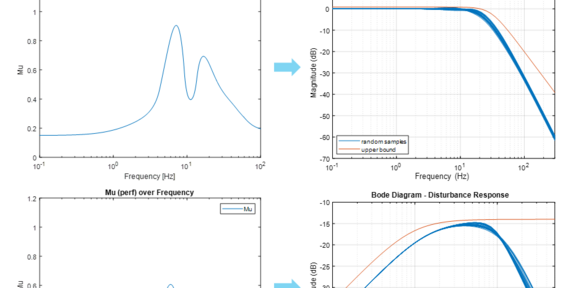
As the control design is typically performed for the nominal system plant model, the question arises if stability and performance are guaranteed in the presence of plant uncertainty. For a systematic analysis of this question parametric and dynamic uncertainty models were defined and introduced into the control loop. Moreover, performance requirements to the command and disturbance response were modeled by respective weighting functions in frequency domain and added to the control system. The thereby resulting uncertain control loop yields the foundation for robust stability and robust performance analysis using the mu-framework. Hereby an optimization problem is solved to find the smallest normalized perturbation, which leads to a violation of stability or performance requirements. The reciprocal value of this smallest normalized perturbation is called the structured singular value (mu). Detailed analyses have proven that the peak mu-value remains below 1 over the entire frequency range, thereby guaranteeing robust stability and robust performance of the designed 2DOF LQG position control.