Comparison of trajectory parameterizations and the consideration of constraints regarding the resulting optimization problems

In many cases trajectory optimization is performed with a discrete set of position samples along the trajectory as decision variables. Several publications apply the parameterization to highway maneuver execution or planning of emergency trajectories. One advantage is the trajectories flexibility, which allows solving a large variety of scenarios. On the other side, not all situations require a parameterization with as many degrees of freedom. Especially during the execution of highway maneuvers, a lower number of decision variables is enough. Since the optimization of position samples relies on finite differences to compute higher-order time derivatives, which is here referred to as Finite Difference Parameterization (FDP), a reduction of samples may not be useful. This motivates the spline parameterization of trajectories. It allows the description of trajectories in a time-continuous manner by a finite set of parameters. Each polynomial spline can be described equivalently by a linear combination of basis functions, which is referred to as B-spline. It adheres to the property of being enclosed by a convex hull. The convex hull property provides the opportunity to guarantee the satisfaction of constraints, which are applied to the trajectory. The replacement of the infinite set of constraints by a finite one based on the convex hull is referred to as B-spline relaxation. In contrast, the commonly used Multiple Interference Test guarantees the satisfaction of constraints only at a finite set of samples along the trajectory.

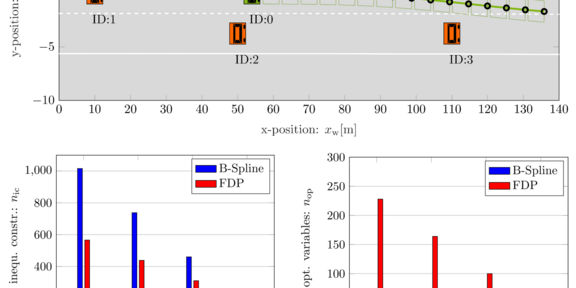
To get an impression of the problem formulations that result from the FDP and the B-spline parameterizations, the number of inequality constraints and optimization variables are compared in dependence on the number of obstacle vehicles in a highway scenario. To avoid collision with obstacle vehicles, the Separating Hyperplane Theorem is utilized, which introduces additional inequalities and optimization variables per obstacle vehicle. The B-spline parameterization, in conjunction with B-spline relaxation, leads to a reduced number of optimization variables in comparison to the FDP parameterization utilizing the Multiple Interference Test. On the other side, the number of inequalities becomes higher for an increasing number of obstacles.

Back